La transformation des objets 3D

L’infographie 3D consiste à modéliser des objets virtuels, en plaçant des vertices dans un espace tridimensionnel. Les vertices seront connectés entre eux par des edges et des faces. Ces derniers font partis du maillage de l’objet modélisé. Cependant il faut pouvoir manipuler le maillage dans l’espace. Pour cela, nous avons besoin d’expliquer quelques principes de manipulation.

La translation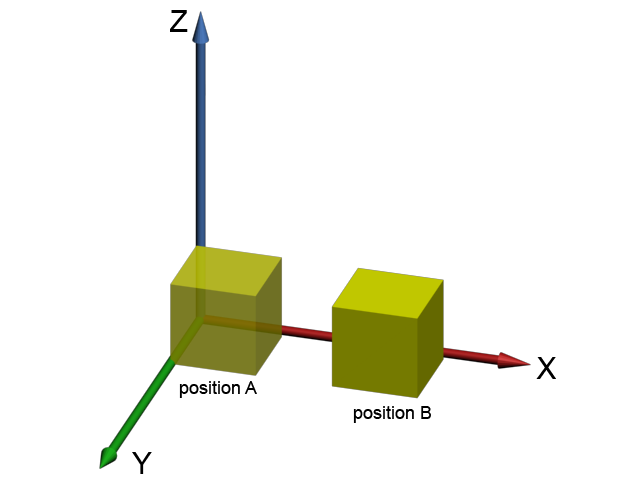

C’est une transformation géométrique qui correspond à un simple déplacement de l’objet sans rotation ni déformation. En mathématique cela consiste en une addition par axe.

Sur cette image, une addition de la position A du cube a été faite sur l’axe des X pour avoir le cube en position B.

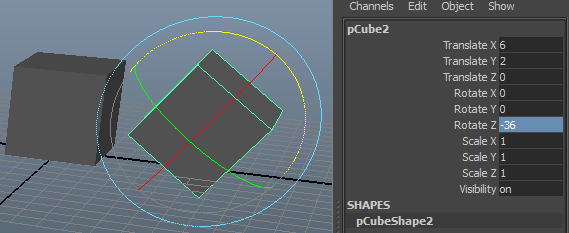
La rotation

Elle consiste à faire pivoter un objet dans l’espace autour d’un axe donné. En effet, la rotation est décomposée en trois mouvements : la rotation autour de l’axe des abscisses, des ordonnées et enfin des cotes. En mathématique cela consiste en un produit matriciel par axe.

ATTENTION : l’ordre des rotations n’est pas commutatif !

L’homothétie

C’est une transformation géométrique qui correspond à un agrandissement ou rétrécissement de l’objet. En mathématique cela consiste en une multiplication par axe. Cette manipulation est appelée avec son terme anglais « scale ».

Les matrices

Matrice 3×3

La matrice 3×3 aussi appelée matrice de rotation permet de faire le calcul d’une rotation d’objet en stockant des données. Ces données sont de deux types, les coordonnées de points ainsi que le coefficient trigonométrique.

Matrice homogène

La matrice homogène est une matrice permettant une multifonction et est donc appelée opérateur « universel ». C’est-à-dire qu’avec le même composant, il peut calculer une translation, une rotation et une homothétie séparément. En plus de cela, il permet la projection pour représenter des scènes en 3D.